Question

Consider the following set of equations, where s, s0, x and r have units of length, t has units of time, v has units of velocity, g and a have units of acceleration, and k is dimensionless. Which one is dimensionally incorrect?

2. v2 = 2 a s + (ksv)/t
3. s = s0 + v t + v^2/a
4. a = g + (k v/t)+ (v2 / s0)
5. t = k (sqrt s/g) + a/v

Answer 1

5

Explanation:

For an equation to be dimensionally correct the dimension of quantities on both sides of equation must be same.

Also, two physically quantities can only be added or subtracted only when their dimension are same.

here all option are dimensionally correct except the 5th option where

dimension of t= [T] whereas dimension of a/v is
`(LT^(-2))/(LT^(-1))`

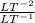
= T^{-1}

since, the dimension of quantities on either sides of equation are not the same the equation is dimensionally is incorrect.