Question

A rotating cup viscometer has an inner cylinder diameter of 2.00 in., and the gap between cups is 0.2 in. The inner cylinder length is 2.50 in. The viscometer is used to obtain viscosity data on a Newtonian liquid. When the inner cylinder rotates at 10 rev/min, the torque on the inner cylinder is measured to be 0.00011 in-lbf. Calculate the viscosity of the fluid. If the fluid density is 850 kg/m^3, calculate the kinematic viscosity

Answer 1

The dynamic viscosity and kinematic viscosity are
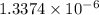`1.3374* 10^(-6)` lb-s/in2 and
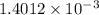`1.4012* 10^(-3)` in2/s.

Step-by-step explanation:

Step1

Given:

Inner diameter is 2.00 in.

Gap between cups is 0.2 in.

Length of the cylinder is 2.5 in.

Rotation of cylinder is 10 rev/min.

Torque is 0.00011 in-lbf.

Density of the fluid is 850 kg/m3 or 0.00095444 slog/in³.

Step2

Calculation:

Tangential force is calculated as follows:

T= Fr

`0.00011 = F*((2)/(2))`

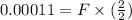
F = 0.00011 lb.

Step3

Tangential velocity is calculated as follows:

`V=\omega r`

`V=((2\pi N)/(60))r`

`V=((2\pi *10)/(60))*1`

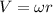
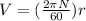
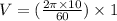
V=1.0472 in/s.

Step4

Apply Newton’s law of viscosity for dynamic viscosity as follows:

`F=\mu A(V)/(y)`

`F=\mu (\pi dl)(V)/(y)`

`0.00011=\mu (\pi*2*2.5)(1.0472)/(0.2)`

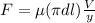
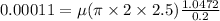
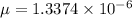`\mu =1.3374* 10^(-6)`lb-s/in².

Step5

Kinematic viscosity is calculated as follows:

`\upsilon=(\mu)/(\rho)`

`\upsilon=(1.3374* 10^(-6))/(0.00095444)`

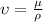
`\upsilon=1.4012* 10^(-3)` in2/s.

Thus, the dynamic viscosity and kinematic viscosity are
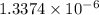`1.3374* 10^(-6)` lb-s/in2 and
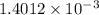`1.4012* 10^(-3)` in2/s.