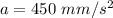Question

A small metal particle passes downward through a fluid medium while being subjected to the attraction of a magnetic field such that its position is observed to be s = (15t^3 - 3t) mm, where t is measured in seconds. Determine (a) the particle's displacement from t = 2 s to t = 4 s, and (b) the velocity and acceleration of the particle when t = 5 s.

Answer 1

a)Δs = 834 mm

b)V=1122 mm/s

`a=450\ mm/s^2`

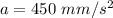
Step-by-step explanation:

Given that

`s = 15t^3 - 3t\ mm`

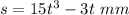
a)

When t= 2 s

`s = 15t^3 - 3t\ mm`

`s = 15* 2^3 - 3* 2\ mm`

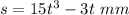
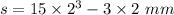
s= 114 mm

At t= 4 s

`s = 15t^3 - 3t\ mm`

`s = 15* 4^3- 3* 4\ mm`

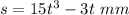
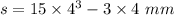
s= 948 mm

So the displacement between 2 s to 4 s

Δs = 948 - 114 mm

Δs = 834 mm

b)

We know that velocity V

`V=(ds)/(dt)`

`(ds)/(dt)=45t^2-3`

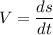
At t= 5 s

`V=45t^2-3`

`V=45* 5^2-3`

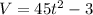
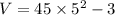
V=1122 mm/s

We know that acceleration a

`a=(d^2s)/(dt^2)`

`(d^2s)/(dt^2)=90t`

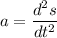
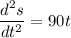
a= 90 t

a = 90 x 5

`a=450\ mm/s^2`