Question

You are given 1000 one dollar bills and 10 envelopes. Put the bills into the envelopes in such a way that someone can ask you for any amount of money from $1 to $1000 (examples - $532, $619, $88, etc.) and you can give it to them through a combination of the envelopes.

Answer 1

We can do it with envelopes with amounts $1,$2,$4,$8,$16,$32,$64,$128,$256 and $489

Explanation:

• Observe that, in binary system, 1023=1111111111. That is, with 10 digits we can express up to number 1023.

This give us the idea to put in each envelope an amount of money equal to the positional value of each digit in the representation of 1023. That is, we will put the bills in envelopes with amounts of money equal to $1,$2,$4,$8,$16,$32,$64,$128,$256 and $512.

However, a little modification must be done, since we do not have $1023, only $1,000. To solve this, the last envelope should have $489 instead of 512.

Observe that:

1. 1+2+4+8+16+32+64+128+256+489=1000
2. Since each one of the first 9 envelopes represents a position in a binary system, we can represent every natural number from zero up to 511.
3. If we want to give an amount "x" which is greater than $511, we can use our $489 envelope. Then we would just need to combine the other 9 to obtain x-489 dollars. Since
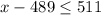   `x-489\leq511`, by 2) we know that this would be possible.