Question

A model rocket is launched from ground level. Its height, h meters above the ground, is a function of time t seconds after launch and is given by the equation . What would be the maximum height, to the nearest meter, attained by the model? (First find the axis of symmetry x= (-b/2a), then plug this value into the equation)

Answer 1

The maximum height attained by the rocket is 240.1 m.

Explanation:

The height above the ground is a function of time t is given by :

`h= -4.9t^2 + 68.6t` ...(1)

We need to find the maximum height of the model. First we find the time of max height using axis of symmetry of the equation as follows :

`x=(-b)/(2a)`

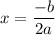
We have, a = -4.9 and b = 68.6

So,

`t=(-(68.6))/(2* -4.9)\\\\=7\ s`

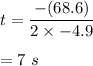
Put t = 7 in equation (1)

`h= -4.9(7)^2 + 68.6(7)\\\\=240.1\ m`

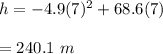
So, the maximum height attained by the rocket is 240.1 m.