Question

Two vertical, parallel clean glass plates are spaced a distance of 2mm apart. if the plates are placed in water, how high will the water rise? if the plates are placed in mercury at 20 degree celcius, how far will the column of mercury be depressed?

Answer 1

Answer with Explanation:

The capillary rise in 2 parallel plates immersed in a liquid is given by the formula

`h=(2\sigma cos(\alpha ))/(\rho gd)`

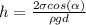
where

`\sigma` is the surface tension of the liquid

`\alpha` is the contact angle of the liquid

`\rho` is density of liquid

'g' is acceleratioj due to gravity

'd' is seperation between thje plates

Part a) When the liquid is water:

For water and glass we have

`\sigma =7.28* 10^(-2)N/m`

`\alpha =0`

`\rho _(w)=1000kg/m^3`

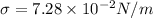
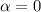
Applying the values we get

`h=(2* 7.28* 10^(-2)cos(0))/(1000* 9.81* 2* 10^(-3))=7.39mm`

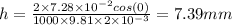
Part b) When the liquid is mercury:

For mercury and glass we have

`\sigma =485.5* 10^(-3)N/m`

`\alpha =138^o`

`\rho _(w)=13.6* 10^(3)kg/m^3`

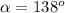
Applying the values we get

`h=(2* 485.5* 10^(-3)cos(138))/(13.6* 1000* 9.81* 2* 10^(-3))=-2.704mm`

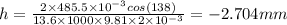
The negative sign indicates that there is depression in mercury in the tube.