Answer:
D. 4 liters
Explanation:
Let x be the volume of first solution and y be the volume of second solution, ( both are in liters )
∵ Total solution = 10 liters,
⇒ x + y = 10 -----(1),
The first solution contained 0.8 liters of acid while the second contained 0.6 liters,
So, the percentage of acid in first solution =
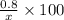
Similarly,
The percentage of acid in second solution =
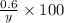
According to the question,
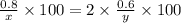
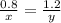
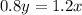
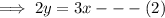
From equation (1),
2x + 2y = 20
2x + 3x = 20
5x = 20
⇒ x = 4
Hence, the volume of the first solution is 4 liters.
OPTION D is correct.