Question

Two solutions of acid were mixed to obtain 10 liters of a new solution. Before they were mixed, the first solution contained 0.8 liters of acid while the second contained 0.6 liters of acid. If the percentage of acid in the first solution was twice that in the second, what was the volume of the first solution?

A. 3 litersB. 3.2 litersC. 3.6 litersD. 4 litersE. 4.2 liters

Answer 1

D. 4 liters

Explanation:

Let x be the volume of first solution and y be the volume of second solution, ( both are in liters )

∵ Total solution = 10 liters,

⇒ x + y = 10 -----(1),

The first solution contained 0.8 liters of acid while the second contained 0.6 liters,

So, the percentage of acid in first solution =
`(0.8)/(x)* 100`

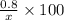
Similarly,

The percentage of acid in second solution =
`(0.6)/(y)* 100`

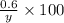
According to the question,

`(0.8)/(x)* 100 = 2* (0.6)/(y)* 100`

`(0.8)/(x)=(1.2)/(y)`

`0.8y = 1.2x`

`\implies 2y = 3x---(2)`

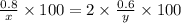
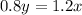
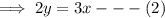
From equation (1),

2x + 2y = 20

2x + 3x = 20

5x = 20

⇒ x = 4

Hence, the volume of the first solution is 4 liters.

OPTION D is correct.