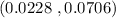Question

The fraction of defective integrated circuits produced in a photolithography process is being studied. A random sample of 300 circuits is tested, revealing 14 defectives. Calculate a 95% two-sided confidence interval on the fraction of defective circuits produced by this particular tool. Round the answers to 4 decimal places.

Answer 1

Answer:
`(0.0228\ ,0.0706)`

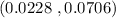
Explanation:

Given : Sample size : n= 300

The sample proportion of defectives :
`\hat{p}=(14)/(300)=0.0467`

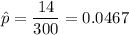
Significance level for 95% confidence level =
`\alpha=1-0.95=0.05`

Critical z-value:
`z_(\alpha/2)=\pm1.96`

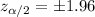
Confidence interval for population proportion :

`\hat{p}\pm z_(\alpha/2)\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

`= 0.0467\pm (1.96)\sqrt{(0.0467(1-0.0467))/(300)}`

`\approx\ 0.0467\pm 0.0239\\\\=(0.0467-0.0239\ , \ 0.0467-0.0239)\\\\=(0.0228\ ,0.0706)`

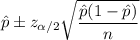
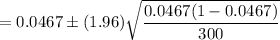
Hence, a 95% two-sided confidence interval on the fraction of defective circuits produced by this particular tool=
`(0.0228\ ,0.0706)`