Question

A hanging spring stretches by 35.0 cm when an object of mass 450 g is hung on it at rest. In this situation, we define its position as x = 0. The object is pulled down an additional 18.0 cm and released from rest to oscillate without friction. What is its position x at a moment 84.4 slater?

Answer 1

- 0.153 m

Step-by-step explanation:

mass, m = 450 g = 0.45 kg

length of the spring, l = 35 cm = 0.35 m

additional stretch, A = 18 cm = 0.18 m

Let ω be the angular frequency and A be the amplitude and k be the spring constant.

F = mg = k l

`k = (mg)/(l)=(0.45 * 9.8)/(0.35)`

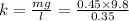
k = 12.6 N/m

`\omega =\sqrt{(k)/(m)}=\sqrt{(12.6)/(0.45)}`

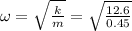
ω = 5.29 rad/s

Use the equation of oscillations

x = A Cosωt

x = 0.18 Cos 5.29 t

Put, t = 84.4 s

x = 0.18 Cos (52.9 x 84.4)

x = - 0.153 m