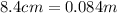Question

a 0.0818 kg salt shaker on a rotating table feels an inward frictional force of 0.108 N when it is moving 0.333m/s. what is the radius of its motion?(unit=m)

Answer 1

0.084

Step-by-step explanation:

Acellus

Answer 2

The required radius of its motion is
`0.084m`.

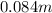Step-by-step explanation:

The formula for calculating the required radius of its motion is given by

`F = (mv^2)/r`

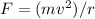
Where m= mass

V= moving velocity

F=frictional force

r = radius of its motion

Then the required radius of its motion is given by

`r =(mv^2)/F`

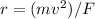
Given that

mas =0.0818 kg

Frictional force= 0.108 N

Moving with Velocity of = 0.333 m/s

radius of its motion =
`([0.0818 kg * (0.333 m/s)^2])/(0.108 N)`

Hence the required radius of its motion is r =
`8.4 cm=0.084m`