Question

. Convert 2AF from hexadecimal to binary. Show your work.

Answer 1

The answer is 2AF₁₆ = 687₁₀ = 1010101111₂.

Step-by-step explanation:

To convert from hexadecimal base system to binary base system, first you can do an intermediate conversion from hexadecimal to decimal using this formula:

`N = x_1 * 16^0 + x_2 * 16^1 + x_3 * 16^2 + x_4 * 16^3+ ... + x_n 16^n^-^1`

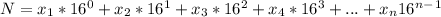
, where position of the x₁ is the rightmost digit of the number and:

• A = 10.
• B = 11.
• C = 12.
• D = 13.
• E = 14.
• F = 15.

2AF₁₆ = 2*16²+A*16¹+F*16⁰ = 512 + 160 + 15 = 687₁₀

Now, transform from decimal to binary the number 687. Divide the number repeatedly by 2, keeping track of each remainder, until we get a quotient that is equal to 0:

• 687 ÷ 2 = 343 + 1;

• 343 ÷ 2 = 171 + 1;

• 171 ÷ 2 = 85 + 1;

• 85 ÷ 2 = 42 + 1;

• 42 ÷ 2 = 21 + 0;

• 21 ÷ 2 = 10 + 1;

• 10 ÷ 2 = 5 + 0;

• 5 ÷ 2 = 2 + 1;

• 2 ÷ 2 = 1 + 0;

• 1 ÷ 2 = 0 + 1;

Now, construct the integer part base 2 representation, by taking the remainders starting from the bottom of the list:

687₁₀ = 1010101111₂