Answer:
a)
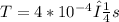
b)
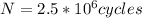
c) 10000 programs.
Step-by-step explanation:
a) We know that the frequency is the inverse of the period, so:
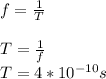
1μs is equal to
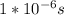
so
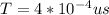
b) If in a second there are 2.5*10^9 cycles:
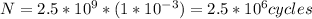
c) we have to make a conversion, we know that a program takes 100*10^(-3) milliseconds, that is, 1*10^(-4) seconds so in 1 second we can execute:
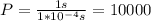
10000 programs.