Answer:
Step-by-step explanation:
mass, m = 43 g = 0.043 kg
L = 81 cm = 0.81 m
frequency, f = 59 Hz
Amplitude, A = 0.35 cm
(a)
Frequency
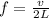
v = 59 x 2 x 0.81 = 95.58 m/s
(b)
Let F be the tension in the string
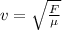
where, μ is mass per unit length
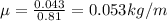
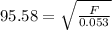
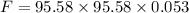
F = 484.18 N
(c)
Maximum velocity
v = ω A = 2 π f A
v = 2 x 3.14 x 59 x 0.0035 = 1.3 m/s
(d)
Maximum acceleration
a = ω² A
a = (2 π f )² x 0.0035
a = ( 2 x 3.14 x 59)² x 0.0035
a = 480.5 m/s^2