Answer:
A) P(Y<70) = 0.6 or 60%
B) P(65<Y<70) = 0.5 or 50%
C) P(Y>65) = 0.9 or 90%
D) Mean = 69 minutes
SD = σ = 2.88 minutes
Step-by-step explanation:
Solution:
let Y is the commuting time between Long Island Railroad from Glen Clove to New York City.
Then,
f ( y) =
 as, it is uniformly distributed between 64 and 74.
as, it is uniformly distributed between 64 and 74.
f (y) = 1/10
now, we have a function so, probability can be found out by the use of integration.
a) P (Y < 70 ) =
 where, a = 70 and b = 64
where, a = 70 and b = 64
by solving this integration, we will get:
P(Y<70) =
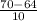 = 0.6
= 0.6
P(Y<70) = 0.6 or 60%
b) P(65<Y<70) = again this can be solved similarly as above, but here a = 70 and b = 65
P(65<Y<70) =

P(65<Y<70) =
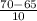 = 0.5
= 0.5
P(65<Y<70) = 0.5 or 50%
c) P(Y>65) = again, this can be solved similarly but here a = 74 and b = 65
P(Y>65) =

P(Y>65) =
 = 0.9
= 0.9
P(Y>65) = 0.9 or 90%
d) Now, we have to calculate the mean and standard deviation of the commuting time.
So,
Mean =
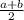
Mean =
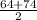
Mean = 69 minutes
Now, for standard deviation:
SD = σ =
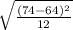
SD = σ = 2.88 minutes