Question

For several years in massachusetts the lottery commission would mail residents coupons for free lotto tickets. to win the jackpot in Massachusetts, you have to correctly guess all six numbers drawn from a pool of 36. What is the expected value of the free lotto ticket if the jackpot is $8,000,000 and there is no splitting of the prize?

Answer 1

Answer: $4.11

Explanation:

Given: To win the jackpot in Massachusetts, we have to correctly guess all six numbers drawn from a pool of 36.

The number of combinations of 6 numbers drawn from a pool of 36 is given by :-

`^(36)C_6=(36!)/(6!(36-6)!)\\\\=(36*35*34*33*32*31*30!)/(6!30!)\\\\=1947792`

Now, the probability of winning the prize =
`\frac{\text{Favorable outcomes}}{\text{Total outcomes}}`

`p=(1)/(1947792)`

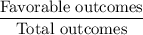
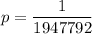
Now, the expected value of the free lotto ticket if the jackpot is $8,000,000 and there is no splitting of the prize =
`p*\text{Amount}`

`(1)/(1947792)*8000000=4.1072147334\approx\$4.11`

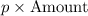
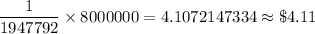
Hence, the expected value of the free lotto ticket if the jackpot is $8,000,000 and there is no splitting of the prize = $4.11