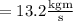Question

In a lab, four balls have the same velocities but different masses.

A 4 column table with 3 rows. The first column is labeled Object with entries Ball A, Ball B, Ball C, Ball D. The second column is labeled Mass in kilograms with entries 1.0, 2.0, 5.0, 7.0. The third column is labeled velocity in meters per second with entries 2.2, 2.2, 2.2, 2.2. The fourth column is labeled Momentum in kilograms times meters per second with entries 2.2, 4.4, 11, 15.
If the mass of ball B triples, its new momentum is kg • .

Answer 1

B

Step-by-step explanation:

Answer 2

New Momentum of Ball B
`=13.2 \frac{\mathrm{kgm}}{\mathrm{s}}`

Step-by-step explanation:

Given:

Mass of Ball A=1kg

Mass of Ball B= 2kg

Mass of Ball C=5kg

Mass of Ball D=7kg

Velocities of A=B=C=D=2.2
`(m)/(s)`

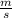
Momentum of Ball A=2.2
`(k g m)/(s)`

Momentum of Ball B=4.4
`(k g m)/(s)`

Momentum of Ball C=11
`(k g m)/(s)`

Momentum of Ball D=15
`(k g m)/(s)`

To Find:

Change in Momentum When of Ball B gets tripled

Solution:

Though all balls have same velocity, thus we get

Velocities of A=B=C=D=2.2
`(m)/(s)`

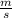
Initial Momentum of Ball B=4.4
`(k g m)/(s)`

If the Mass of Ball B gets tripled;

We get New Mass of Ball B=3×Actual Mass of the ball

=3×2=6kg

Thus we get Mass of Ball B=6kg

According to the formula,

Change in momentum of Ball B
`\Delta p=m * \Delta v`

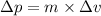
Where
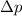`\Delta p`=change in momentum

m=mass of the ball B

`\Delta v`=change in velocity ball B

And
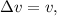`\Delta v=v,` since all balls, have same velocity

Thus the above equation, changes to

`\Delta p=m * v`

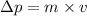
Substitute all the values in the above equation we get

`\Delta p=6 * 2.2`

`=13.2 \frac{\mathrm{kgm}}{\mathrm{s}}`

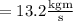
Result:

Thus the New Momentum of ball B
`=13.2 \frac{\mathrm{kgm}}{\mathrm{s}}`