Question

Two cars leave an intersection at the same time. Car A travels north at 35 miles per hour, and Car B travels east at 65 miles per hour. Find the distance (in miles) between the two cars at time t, where t represents the number of minutes elapsed since the cars left the intersection.

Answer 1

The distance between both cars at any time t in minutes, is given by the expression:

`D=\sqrt{(5450)/(3600)}*t`

Which can be approximately

`D=1,23*t`

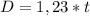
Explanation:

Distance is given by the expression:

1.
`D=v*t`

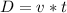
Where D is distance, v is speed or velocity, and t is time.

We will find first, the distance of each car to the intersection, by replacing the known values on the equation 1:

Distance of the car A to the intersection, at any time t in minutes:

2.
`y[miles]=35(miles)/(h)*t[min] *(1 h)/(60 min)`

Distance of the car B to the intersection, at any time t in minutes:

3.
`x[miles]=65(miles)/(h)*t[min] *(1 h)/(60 min)`

The expression
`(1 h)/(60 min)` will work to convert time from minutes to hours, so it can be properly computed.

You will find a diagram attached to the response, to understand where are this expressions coming from. Now, as one car went north and the other one went east, the distance between both cars is given by a pythagorical expression.

4.
`D=√(x^2+y^2)`

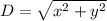
Replacing 2 and 3 in 4 and omiting the units, for ease of computing:

5.
`D=\sqrt{((65t)/(60) )^2+((35t)/(60) )^2}`

Computing 5:

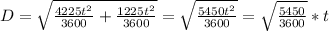`D=\sqrt{(4225t^2)/(3600)+(1225t^2)/(3600)}=\sqrt{(5450t^2)/(3600)}=\sqrt{(5450)/(3600) }*t` ≅ 1,23*t