Answer:
The probability is 0.9993
Explanation:
This situation follows a Binomial distribution in which we have:
- n identical and independent events: this are the 66 adult smartphone users.
- Two possibles results: success or fail. These are if they use the smartphone in meeting or classes or if they don't.
- Probability p of success: This is the 52% of adults that use them in meeting and classes.
So, the probability that x of the n elements are success is given by:
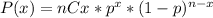
That means that the probability that x adults from the 66 use their smartphone in meeting or classes is:
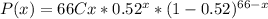
Where 66Cx is calculated as:

Then, the probability that at least 22 of them use their smartphone in meeting or classes is:
P = P(22) + P(23) + P(24) +... + P(64) + P(65) + P(66)
Therefore, replacing x for each number from 22 to 66 on the equation of P(x), and making a sum with all the probabilities, we get that:
P = 0.9993