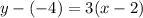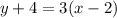Answer:
Slope-intercept form: is y=3x-10.
Point-slope form: y+4=3(x-2).
Standard form: 3x-y=10.
Explanation:
Slope-intercept form is y=mx+b where m is the slope and b is the y-intercept.
A line parallel to y=3x+2 will be of the form y=3x+b where b is not 2.
To find b, we will use that our line goes through (2,-4).
-4=3(2)+b
-4=6+b
Subtract 6 on both sides:
-4-6=b
-10=b
The the line we are looking for in slope-intercept form is y=3x-10.
Standard form is ax+by=c.
y=3x-10
Add 10 on both sides:
10+y=3x
Subtract y on both sides:
10=3x-y
So the equation in standard form is 3x-y=10.
Point-slope form is
 .
.