Question

After the NEAR spacecraft passed Mathilde, on several occasions rocket propellant was expelled to adjust the spacecraft's momentum in order to follow a path that would approach the asteroid Eros, the final destination for the mission. After getting close to Eros, further small adjustments made the momentum just right to give a circular orbit of radius 45 km (45 × 103 m) around the asteroid. So much propellant had been used that the final mass of the spacecraft while in circular orbit around Eros was only 545 kg. The spacecraft took 1.04 days to make one complete circular orbit around Eros. Calculate what the mass of Eros must be:

Answer 1

Mamaste cuzzo alv el mundo #TrokitasDelValle956

Answer 2

The mass of Eros must be approximately
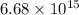`\(6.68 * 10^(15)\)` kilograms.

How to determine this?

Certainly, let's rearrange and rewrite the steps for determining the mass of the asteroid Eros:

Given:

Radius of circular orbit
`(\(r\)) = 45 * 10^3` meters

Period of orbit
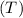`(\(T\))` = 1.04 days = 89,856 seconds

Mass of spacecraft
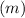`(\(m\))` = 545 kg

Gravitational constant (
`\(G\))` =
`\(6.67430 * 10^(-11)\) m^3 kg^-1 s^-2`

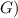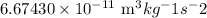
Calculate the velocity (\(v\)) of the spacecraft in the circular orbit:

`\[ v = \frac{{2 \pi \cdot r}}{{T}} \]`

`\[ v \approx \frac{{2 \pi \cdot 45 * 10^3 \, \text{m}}}{{89,856 \, \text{s}}} \]`

`\[ v \approx 3,019.98 \, \text{m/s} \]`

2. Use the formula to determine the mass (\(M\)) of the asteroid Eros:

`\[ M = \frac{{v^2 \cdot r}}{{G}} \]`

`\[ M = \frac{{(3,019.98 \, \text{m/s})^2 \cdot (45 * 10^3 \, \text{m})}}{{6.67430 * 10^(-11) \, \text{m}^3 \, \text{kg}^(-1) \, \text{s}^(-2)}} \]`

`\[ M \approx 6.68 * 10^(15) \, \text{kg} \]`

Hence, the estimated mass of the asteroid Eros is approximately
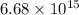`\(6.68 * 10^(15)\)` kilograms.