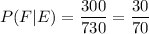Question

Suppose that E and F are two events and that N(E and F)=300 and N(E)=730. What is P(F|E)?

Answer 1

`\displaystyle(30)/(73)`

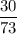
Explanation:

The formula of conditional probability is:

`\displaystyle P(F|E)=(P(E \cap F))/(P(E))`

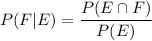
And if we called N(U) the total number of possible outcomes, then remember by definition of probability:

`\displaystyle P(E \cap F)=(N(E \cap F))/(N(U))\\\displaystyle P(E)=(N(E))/(N(U))`

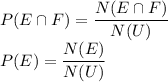
Then plugging them into the formula of conditional probability we get:

`\displaystyle P(F|E)=((N(E \cap F))/(N(U)))/((N(E))/(N(U)))`

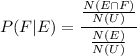
Then we simplify and we get:

`\displaystyle P(F|E)=(N(E \cap F))/(N(E))`

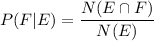
We just plug the given info and we get:

`\displaystyle P(F|E)=(300)/(730)=(30)/(70)`