Question

A certain law firm consists of 4 senior partners and 6 junior partners. How many different groups of 3 partners can be formed in which at least one member of the group is a senior partner? (Two groups are considered different if at least one group member is different.)

Answer 1

There are 100 different groups that can be formed.

Explanation:

We will define:

• 
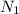  `N_1`=The number of different groups of 3 partners that can be formed in which exactly one member of the group is a senior partner.
• 
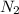  `N_2`=The number of different groups of 3 partners that can be formed in which exactly two members of the group are senior partners.
• 
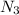  `N_3`=The number of different groups of 3 partners that can be formed in which exactly three members of the group are senior partners.

Observe that the quantity we are looking for is
`N_1+N_2+N_3`, then we will compute them.

• 
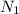  `N_1`. In this case we want to choose 1 senior partner between 4 and 2 junior partners between 6. Since the choices are independent, the numbers of ways to do this is given by
  `{4\choose 1}{6\choose 2}=(4!)/(3!)(6!)/(4!2!) =(6!)/(3!2!) =60.`

• 
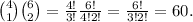
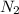  `N_2`. In this case we want to choose 2 senior partners between 4 and 1 junior partner between 6. Since the choices are independent, the numbers of ways to do this is given by
  `{4\choose 2}{6\choose 1}=(4!)/(2!2!)(6!)/(5!) =36.`

• 
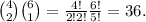
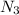  `N_3`. In this case we want to choose 3 senior partners between 4 and 0 junior partners between 6. Since the choices are independent, the numbers of ways to do this is given by
  `{4\choose 3}{6\choose 0}=(4!)/(3!)=4.`

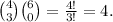
Therefore:

`N_1+N_2+N_3=60+36+4=100.`