Two consecutive numbers are x and x+1.
Clearly, x is the lesser, and x+1 is the largest.
The sum of their squares is
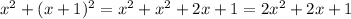
If we add this sum and the lesser we have
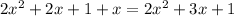
We want this quantity to be 21, so we have

The solutions of this equation are

Since we want integers, the numbers are -4 and -3.