Answer:
The speed of the block is 4.96 m/s.
Step-by-step explanation:
Given that.
Mass of block = 1.00 kg
Spring constant = 500 N/m
Position
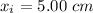
Coefficient of friction = 0.350
(A). We need to calculate the speed the block has as it passes through equilibrium if the horizontal surface is friction less
Using formula of kinetic energy and potential energy
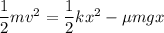
Put the value into the formula
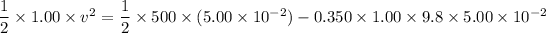
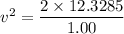
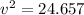
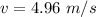
Hence, The speed of the block is 4.96 m/s.