Answer:
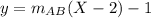
Explanation:
When two lines are parallel means that their slopes are equal. Therefore the line AB will have same slope to a parallel second line,
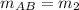 .
.
To obtain the slope from the line AB, we need two points, so the general equation will be:
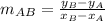
The typical equation of a line is written as y = mx + b
The second line will pass through point (2, -1), so we can substitute:
y2 = mX2 + b
-1 =
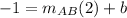 (2) + b
(2) + b
then the interception is
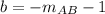
Now to obtain a general equation for the second parallel line will be:
y =
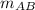 X + b
X + b
y =
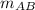 X -
X -
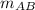 (2)-1
(2)-1
Finally we get:
y =
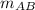 (x-2)-1
(x-2)-1