Question

Three pumpkins and two squash weigh 27.5 pounds. Four pumpkins and three squash weigh 37.5 pounds. Each pumpkin weighs the same as the other pumpkins, and each squash weighs the same as the other squash. How much does each pumpkin weigh? How much does each squash weigh?

Answer 1

Each pumpkin weighs 7.5 pounds.

Each squash weighs 2.5 pounds.

Explanation:

Let x represent weight of each pumpkin and y represent weight of each squash.

We have been given three pumpkins and two squash weigh 27.5 pounds. We can represent this information in an equation as:

`3x+2y=27.5...(1)`

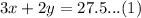
We are also told that four pumpkins and three squash weigh 37.5 pounds. We can represent this information in an equation as:

`4x+3y=37.5...(2)`

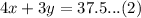
From equation (1), we will get:

`y=(27.5-3x)/(2)`

Substitute this value in equation (2):

`4x+3((27.5-3x)/(2))=37.5`

`4x+1.5(27.5-3x)=37.5`

`4x+41.25-4.5x=37.5`

`41.25-0.5x=37.5`

`41.25-41.25-0.5x=37.5-41.25`

`-0.5x=-3.75`

`(-0.5x)/(-0.5)=(-3.75)/(-0.5)`

`x=7.5`

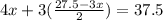
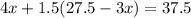
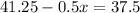
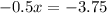
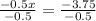
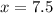
Therefore, the weight of each pumpkin is 7.5 pounds.

Substitute
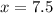`x=7.5` in equation (1):

`3(7.5)+2y=27.5`

`22.5+2y=27.5`

`22.5-22.5+2y=27.5-22.5`

`2y=5`

`(2y)/(2)=(5)/(2)`

`y=2.5`

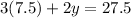
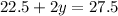
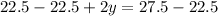
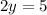
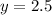
Therefore, the weight of each squash is 2.5 pounds.