Answer:
Necklace: $85,
Notebook: $8.5
Scarf: $51
Necklace costs $76.5 more than the notebook.
Explanation:
Let x represent cost of the necklace.
We have been given that Elise saved $184. She bought a scarf, a necklace, and a notebook.
The scarf cost three-fifths the cost of the necklace, so the cost of scarf would be
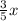 .
.
The notebook was one-sixth as much as the scarf, so the cost of notebook would be
 .
.
We are also told that she still have $39.50, so the cost of all items would be:

Now, we will equate cost of all items equal to $144.5 as:
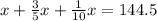
Make a common denominator:
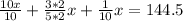
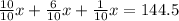
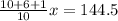
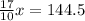


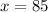
Therefore, the cost of necklace is $85.
Cost of notebook:
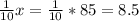
Therefore, the cost of notebook is $8.5.
Cost of scarf:
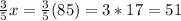 .
.
Therefore, the cost of scarf is $51.
To find the difference between cost of necklace and notebook, we will subtract $8.5 from $85 as:
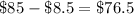
Therefore, necklace costs $76.5 more than the notebook.