Answer:
see explanation
Explanation:
The terms of a geometric progression are
a, ar, ar², ar³, ...... , a

Thus the sum of the third and fourth is
ar² + ar³ = 108 → (1)
The sum of the fourth and fifth is
ar³ + a
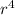 = 324 → (2)
= 324 → (2)
Factorise both equations
ar²(1 + r) = 108 → (3)
ar³(1 + r) = 324 → (4)
Divide (4) by (3)
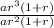 =
=
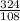
Cancelling (1 + r) , a and r, gives
r = 3
Substitute r = 3 into (3) and solve for a
9a(4) = 108
36a = 108 ( divide both sides by 36 )
a = 3
The n th term is
 = a
= a
 with a = 3 and r = 3, hence
with a = 3 and r = 3, hence
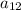 = 3
= 3
 = 531441
= 531441