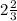Question

Subtract 5 from 1/3 of 23.

Write an expression to match, and then evaluate.

Answer 1

`f(x)=(1)/(3)x-5`

Explanation:

There is no much information about it. So, I guess you can write it as a Slope Intercept Equation:

`f(x)=(1)/(3)x-5`

Let's evaluate 23

`f(23)=(1)/(3)(23)-5=(8)/(3)` ≈2.67

Also you can write other expressions like this:

`f(x)=23x-5`

or

`f(x)=(23)(1)/(3)-x`

Answer 2

Expression:
`(23*(1)/(3))-5`

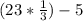
After evaluate:
`2(2)/(3)`

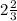
Explanation:

Notice that the exercise says "
`(1)/(3)` of 23". This is:

`23*(1)/(3)`

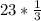
According to the exercise, you must "Subtract 5 from
`(1)/(3)` of 23"; knowing this you can write the following expression:

`(23*(1)/(3))-5`

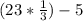
In order to evaluate the expression, the first step you need to apply is to solve the multiplication inside the parentheses:

`((23*1)/(3))-5=(23)/(3)-5`

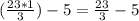
Now you need to solve the subtraction.

Since the denominator of
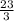`(23)/(3)` is 3 and the denominator of 5 is 1 (
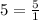`5=(5)/(1)`), the Least Common Denominator (LCD) is 3. Then:

`=(23-15)/(3)=(8)/(3)`

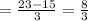
Finally, you can convert this improper fraction to a mixed number. The steps are:

• Divide the numerator 8 by the denominator 3. You will get 2, with a remainder of 2.
• Use 2 as the whole number, and the remainder 2 as the numerator.
• The denominator does not change. It's 3.

Then, you get:

`2(2)/(3)`