Answer : The correct option is, (x-y+1=0)
Step-by-step explanation :
The general form for the formation of a linear equation is:
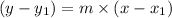 .............(1)
.............(1)
where,
x and y are the coordinates of x-axis and y-axis respectively.
m is slope of line.
First we have to calculate the slope of line.
Formula used :

Here,
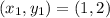 and
and

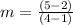
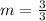
m = 1
Now put the value of slope in equation 1, we get the linear equation.
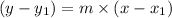
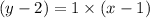

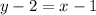
Now rearranging the terms, we get:
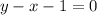
or,
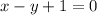
From the given options we conclude that the option (x-y+1=0) is an equation of the given line in standard form.
Hence, the correct option is, (x-y+1=0)