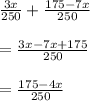Question

An urn contains 10 balls: 7 red and 3 blue. A second urn contains 25 red balls and an unknown number of blue balls. A single ball is drawn at random from each urn. The probability that the balls are the same color is ________

Answer 1

The probability that the balls are the same color is
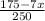`(175-7x)/(250)` where x is the number of blue balls in the second urn

Explanation:

Let's call x the number of blue balls in the second urn. Since there are 25 ball in this urn, the number of red balls would be 25 - x.

Now, we're looking for the probability that the balls are the same color, this means, that both balls are either blue OR red. (since we're using "or", this gives us the clue that we will sum up both probabilities.

1) P(both balls are the same color) = P(both balls are blue) + P( both balls are red).

2) Now we will find what is the probability that both balls are blue (this will be a multiplication since we need that ball 1 is blue AND ball 2 is blue:

P(both balls are blue) = P(ball 1 is blue) x P(ball 2 is blue)

P(both balls are blue) =
`((3)/(10) )((x)/(25) )` =
`(3x)/(250)`

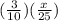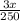
3) To find what is the probability that both balls are red, the process is similar than when both are blue.

P(both balls are red) = P(ball 1 is red) x P(ball 2 is red)

P(both balls are red) =
`((7)/(10) )((25-x)/(25) )`=
`(175-7x)/(250)`

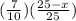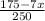
4) Going back to 1) and substituting:

P(both balls are the same color) =
`(3x)/(250) +(175-7x)/(250) \\ \\ = (3x-7x+175)/(250) \\ \\=(175-4x)/(250)`