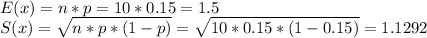Question

Of all the weld failures in a certain assembly, 85% of them occur in the weld metal itself. Asample of 10 weld failures is examined. Assume independence of weld failures.(a) What is the probability thatfewer than fourof them are base metal failures?(b) What is the probability thatat least nineof them are base metal failures?(c) Find themeanandstandard deviationof the number of base metal failures

Answer 1

(a) The probability is 0.95

(b) The probability is 0

(c) The mean is 1.5 base metal failures and the standard deviation is 1.1292 base metal failures

Explanation:

This experiment follows a Binomial distribution in which we have n identical and independent events with two possibles results: success and failure. Then, the probability that x of the n events are success is given by:

`P(x)=nCx*p^(x)*(1-p)^(n-x)`

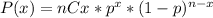
Where p is the probability of success. Additionally, nCx is calculated as:

`nCx=(n!)/(x!(n-x)!)`

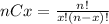
So, in this case we have 10 weld failures with a probability 0.85 that it is a weld metal failure and a probability of 0.15 that it is a base metal failure. Then, we are going to call success if the fail is in the base metal so p is equal to 0.15 and n is equal to 10.

(a) The probability that fewer than four of them are base metal failure is the sum of probabilities that 0, 1, 2 and 3 of the 10 weld failures are base metal failures. This is:

P = P(0) + P(1) + P(2) + P(3)

`P=(10C0*0.15^(0) *0.85^(10) )+(10C1*0.15^(1) *0.85^(9) )+(10C2*0.15^(2) *0.85^(8) )+(10C3*0.15^(3) *0.85^(7) )`

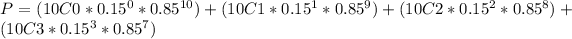
P = 0.1969 + 0.3474 + 0.2759 + 0.1298

P = 0.95

(b) The probability that at least nine of them are base metal failures is the sum of probabilities that 9 and 10 of the 10 weld failures are base metal failures. This is:

P = P(9) + P(10)

`P=(10C9*0.15^(9) *0.85^(1) )+(10C10*0.15^(10) *0.85^(0) )`

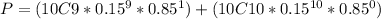
P ≈ 0

(c) The mean E(x) and standard deviation S(x) for variables that follows a Binomial distributions are:

`E(x) =n*p\\S(x) =√(n*p*(1-p))`

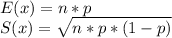
Then, the values of the mean and standard deviation of the number of base metal failures are:

`E(x) =n*p=10*0.15=1.5 \\S(x) =√(n*p*(1-p))=√(10*0.15*(1-0.15))=1.1292`