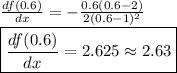Answer:
The rate of change of the number of vehicles waiting with respect to the traffic intensity for the intensities are:
a) 0.52
b) 2.63
Explanation:
The rate of change of a function at a given point P can be obtained by evaluating the 1st derivative of the function in P. Thus,
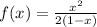
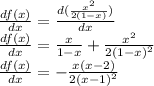
Now for we just need to evaluate in each of the given points
a)
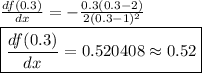
b)