Question

As voters exit the polls, you ask a representative random sample of voters if they voted for a proposition. If the true percentage of voters who vote for the proposition is 63%, what is the probability that, in your sample, exactly 5 do not voted for the proposition before 2 voted for the proposition? The probability is

Answer 1

The probability is 0.057797

Explanation:

Consider the provided information.

It is given that true percentage of voters who vote for the proposition is 63%,

Let p is probability of success.

According to the binomial distribution:

`P(x;p,n)=^nC_x(p)^x(1-p)^((n-x))`

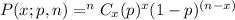
Substitute n=7, p=0.63 and x=2 in the above formula.

`P(x;p,n)=^7C_2(0.63)^2(1-0.63)^((7-2))`

`P(x;p,n)=(7!)/(2!5!)(0.3969)(0.37)^(5)\\P(x;p,n)=21(0.3969)(0.37)^(5)\\P(x;p,n)=0.0577974947199\\P(x;p,n)\approx0.057797`

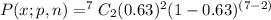
Hence, the probability is 0.057797