Answer:
The probability is 0.057797
Explanation:
Consider the provided information.
It is given that true percentage of voters who vote for the proposition is 63%,
Let p is probability of success.
According to the binomial distribution:
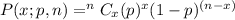
Substitute n=7, p=0.63 and x=2 in the above formula.
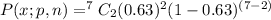

Hence, the probability is 0.057797