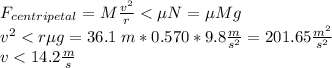Question

A crate of eggs is located in the middle of the flat bed of a pickup truck as the truck negotiates a curve in the flat road. The curve may be regarded as an arc of a circle of radius 36.1 m. If the coefficient of static friction between crate and truck is 0.570, how fast can the truck be moving without the crate sliding?

Answer 1

`v_(max)=14.2(m)/(s)`

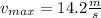
Step-by-step explanation:

Hi!

If the crate is not sliding, its trajectory is the arc with 36.1 m radius. Then the crate has a centripetal acceleration:

`a_c= (v^2)/(r) \\r = radius\\v = tangential \; velocity`

The centripetal force acting on the crate is the static friction force between crate and truck. The maximum value of this force is:

`F_(max) = \mu N\\\mu = 0.570=static\;friction \;coefficient\\N =normal\; force\\`

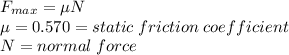
The normal force has a magnitude equal to the weight of the crate:

`N=mg`

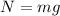
Then the condition for not sliding is:

`F_(centripetal) = M(v^2)/(r)<\mu N=\mu Mg\\ v^2<r \mu g = 36.1\;m*0.570*9.8(m)/(s^2)= 201.65 (m^2)/(s^2)\\ v<14.2(m)/(s)`