Question

A centrifugal pump is installed in a pipeline to raise water14.9 m into an elevated holding tank. The length of the ductileiron pipeline (f=0.019) connecting the reservoirs is 22.4 m. Thepipe is 5.0 cm in diameter and the performance curve of the pump isgiven by Hp =23.9?7.59Q2 where Hp is in meters, Q is in liters persecond, and the equation is valid for flows up to 1.5 L/s. Usingthis pump, what flow do you expect in the pipeline if minor lossesare ignored? What pump head is required for this flow?

Answer 1

Hp = 23.86 m

Hence, 23.86 m head pump is required for this flow.

Step-by-step explanation:

Solution:

Data Given:

Elevation = Z = 14.9 m

Friction of the ductile iron pipe = f = 0.019

Length of the ductile iron pipe connecting the reservoirs = 22.4 m

Diameter of the Pipe = D = 0.5 cm

Radius of the Pipe = r = D/2 = 0.25 cm

Performance Curve of the Pump = Hp = 23.9 - 7.59
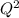`Q^(2)` , where Hp is in meters.

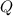`Q^{}` is in Liters/second and equation is valid for 1.5 L/s

We are asked to find out the pump head required for this flow.

We need to apply the energy equation for this problem:

Energy Equation:

`(P1)/(\beta 1) + (v1^(2) )/(2g) + Z1 + Hp = (P2)/(\beta 2) + (v2^(2) )/(2g) + Z2 + H_(L)`

where,
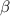`\beta` = specific weight of the fluid.

v1 = 0

P1 = P2 = P

Z1 = 0

Z2 = 14.9

Hence,

New equation is:

`Hp = (v2^(2) )/(2g) + Z2 + H_(L)`

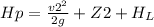
And

`H_(L)` =
`(fLv^(2) )/(2gD)`

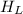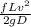
So,

`Hp = (v2^(2) )/(2g) + Z2 + (fLv^(2) )/(2gD)`

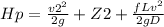
Now, converting formula of v into terms of Q, we get

Hp = 23.9 - 7.59
`Q^(2)`

`Hp = (Q2^(2) )/(2(9.81)((\pi )/(4)(0.05^(2)))^(2) ) + 14.9 + ((0.09)(22.4)Q^(2) )/(12.1(0.05)^(2) )`

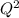
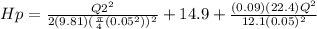
23.9 - 7.59
`Q^(2)` =
`(Q2^(2) )/(2(9.81)((\pi )/(4)(0.05^(2)))^(2) ) + 14.9 + ((0.09)(22.4)Q^(2) )/(12.1(0.05)^(2) )`

Solving for Q, we will get

9 - 7.59
`Q^(2)` = 13233.71
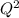`Q^(2)` + 112555.37
`Q^(2)`

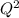
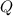`Q^{}` = 7.154 x
`10^(-5)`
`m^(3)/s`

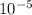
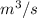
Converting it into L/s

Q = 0.0715 L/s

Putting this value of Q into the Hp equation to get the required answer:

Hp = 23.9 - 7.59
`Q^(2)`

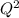
Hp = 23.9 - 7.59 x
`0.0715^(2)`

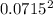
Hp = Pump head

Hp = 23.86 m

Hence, 23.86 m head pump is required for this flow.