Answer:
They are 959.70 m apart after 1.5 h
Step-by-step explanation:
Lets explain how to solve the problem
The given is:
→ The velocity of the 1st airplane is 740 m/h at a heading of 25.3°
→ The velocity of 2nd airplane is 570 m/h at a heading 82°
→ We need to find how far apart they are after 1.5 h
At first lets find the distance of each one after 1.5 h
→ d = v × t
→
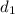 = 740 × 1.5 = 1110 m
= 740 × 1.5 = 1110 m
→
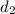 = 570 × 1.5 = 855 m
= 570 × 1.5 = 855 m
Assume that these two distance are two side of a triangle.
The angle between the two sides is the difference between their
heading.
The heading of the 1st airplane is 25.3° and the heading of the second
airplane is 82°
The angle between their distances = 82 - 25.3 = 56.7°
The angle between the two sides of the triangle is 56.7°
Lets use cosine rule to find the 3rd side of the triangle
→
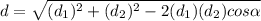
→
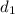 = 1110 ,
= 1110 ,
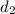 = 855 , α = 56.7
= 855 , α = 56.7
Substitute these values in the rule
→
 m
m
d represents the distance between the two airplanes after 1.5 h
They are 959.70 m apart after 1.5 h