Question

3. Why do cube roots of negative numbers exist in the set of real numbers,

but square roots of negative numbers do not?
A. The square root of a number, positive or negative, is always negative.
However, the cube of a negative number does not exist.
B. The square root of a number, positive or negative, is always positive.
However, the cube of a negative number is positive.
C. The square root of a number, positive or negative, is always positive.
However, the cube of a negative number is negative.
D. The square root of a number, positive or negative, is always positive.
However, the cube of a negative number does not exist.

Answer 1

I'd go with

C. The square root of a number, positive or negative, is always positive.

However, the cube of a negative number is negative.

------

That's not totally true and it's a bit off the point. The square root of a negative number isn't a positive number, it's a positive number times i.

Even that's not totally true. We need to distinguish between a square root and the principal square root function. What's true is every non zero complex number has two square roots, negations of each other.
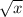`√(x)`, the radical sign applied to a real number, is a function, because we define it to be by choosing one of the square roots as the principal square root.

The right answer would be more like

E. The square of a non-zero real number is always a positive real, so considering the inverse, negative reals don't have real square roots. The cube of a real number has the same sign as the original number, so again considering the inverse, negative reals do have real cube roots.

Answer 2

C. The square root of a number, positive or negative, is always positive. However, the cube of a negative number is negative.

Explanation:

Of the choices offered, the one shown above is the only one that remotely makes any sense. Its description of square roots is erroneous, however.

The square root of a number n is the solution to the equation ...

x² = n

The function f(x) = x² has a range that only includes non-negative numbers, so the square root of a negative number does not exist. (Your answer choice says it is positive. It is actually non-existent among real numbers.)

On the other hand, the cube root of a number n is the solution to the equation ...

x³ = n

Since f(x) = x³ has a range that includes all real numbers, the cube root of n exists for all real numbers. (It is negative for negative values of n.)

_____

Comment on answer wording

The answer wording would be correct if the word "root" were left out.