Question

A steel ball is dropped from a building's roof and passes a window, taking 0.14 s to fall from the top to the bottom of the window, a distance of 1.20 m. It then falls to a sidewalk and bounces back past the window, moving from bottom to top in 0.14 s. Assume that the upward flight is an exact reverse of the fall. The time the ball spends below the bottom of the window is 2.22 s. How tall is the building?

Answer 1

The building is 20.68m high.

Step-by-step explanation:

In order to solve this problem we must first do a drawing of what the situation looks like. (Look at the attached picture). Then, we determine what was the velocity of the ball when it reached the top of the window (let's call this
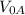`V_(0A)` and when it reached the bottom of the window (let's call this
`V_(0B)`. We can start by finding the velocity the ball has at the top of the window
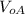`V_(oA)` when it's falling.

In order to do so, we can use the following equation:

`\updelta y=V_(0A)t+(1)/(2) at^(2)`

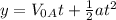
We can now solve this equation for
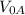`V_(0A)` so we get:

`v_(0A)=(\updelta y-(1)/(2) at^(2))/(t)`

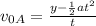
or when simplified we get:

`v_(0A)=(2\updelta y-at^(2))/(2t)`

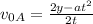
now we can substitute values in the formula so we get:

`v_(0A)=(2(-1.20m)-(-9.8m/s^(2))(0.14s)^(2))/(2(0.14))`

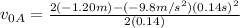
and solve:

`v_(0A)=-7.886m/s`

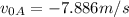
Once we got the first velocity, we can proceed and find the second velocity.

We can find that by using the following formula:

`a=(V_(f)^(2)-V_(0)^(2))/(2y)`

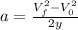
So now we can solve for
`V_(f)`

When solving for
`V_(f)`, we get the following formula:

`V_f=\sqrt{2ya+V_(0)^(2)}`

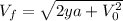
So we can now substitute some values.

`V_(0B)=\sqrt{2(-1.20m)(-9.8m/s\{2})+(-7.885m/s)^(2)}`

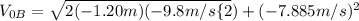
When solving this equation we get an answer of:

`V_(0B)=-9.257m/s`

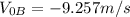
Once we got those velocities, we can use them to find the distance from the roof to the highest part of the window and the distance between the

lowest part of the window and the floor.

Let's start with the top portion of the window:

`y=(V_(f)^(2)-V_(0)^(2))/(2A)`

in this case, the initial velocity is 0 because we are dropping the ball from the roof. So we can now substitute values so we get:

`y=((-7.885m/s)^(2)-(0)^(2))/(2(-9.8m/s^(2))`

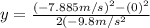
when solving this for y we get:

y=-3.17m

Now, we can find the height between the lowest part of the window and the floor, so we get:

`\updelta y=V_(0B)t+(1)/(2) at^(2)`

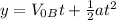
In this case the time is 1.11s because it's half of the total time the ball is beneath the window when it's falling. So when substituting values we get:

`\updelta y=(-9.257m/s^(2))(1.11s)+(1)/(2) (-9.8m/s^(2))(1.11s)^(2)`

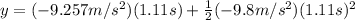
When solving that expression we get that:

`\updelta y=-16.31m`

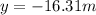
so now we have enough information to solve the problem, notice that the heights appear as negative. This is because the bal is falling at this time. Since we only care about the magnitud, we can make them positive.

So in order to find the height of the building, we must ad the three lengths we just found, so we get:

h=3.17m+1.20m+16.31m=20.68m

So the building has a height of 20.68m