Answer:
There is not enough statistical evidence to state that the mean score on one-tailed hypothesis test questions is higher than the mean score on two-tailed hypothesis test questions.
Explanation:
To solve this problem, we run a hypothesis test about the difference of population means.

The appropriate hypothesis system for this situation is:
![H_0:\mu_X-\mu_Y=0\\H_a:\mu_X-\mu_Y > 0\\\\$Difference of means in the null hypothesis is:\\\mu_X-\mu_Y=M_0=0\\\\$The test statistic is $Z=\frac{[( \bar X-\bar Y)-M_0]}{\sqrt{(\sigma^2_X)/(n_X)+(\sigma^2_Y)/(n_Y)}}\\](https://img.qammunity.org/2020/formulas/mathematics/college/ivofqodqop4ingi2pthdwe24329m0fef25.png)
![$$The calculated statistic is Z_c=\frac{[(7.79-7.64)-0]}{\sqrt{(1.06^2)/(80)+(1.31^2)/(80)}}=0.79616\\\\p-value = P(Z \geq Z_c)=0.42594\\\\](https://img.qammunity.org/2020/formulas/mathematics/college/q12vfyvqcyj99lty0nu4rzlms9jmvvep0i.png)
Since, the calculated statistic
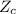 is less than critical
is less than critical
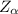 , the null hypothesis do not should be rejected. There is not enough statistical evidence to state that the mean score on one-tailed hypothesis test questions is higher than the mean score on two-tailed hypothesis test questions.
, the null hypothesis do not should be rejected. There is not enough statistical evidence to state that the mean score on one-tailed hypothesis test questions is higher than the mean score on two-tailed hypothesis test questions.