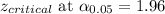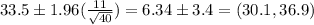Answer:
Confidence interval: (30.1,36.9)
Explanation:
We are given the following data set:
35.3,30.5,37.4,26.5,13.0,49.9,28.8,44.0,61.6,0.5,40.5,34.9,47.9,36.6,24.1,39.8,47.8,18.5,36.6,39.2,14.5,37.3,40.5,49.3,45.5,28.3,19.5,5.6,52.6,41.4,45.3,39.0,33.7,29.4,14.5,40.1,33.7,36.9,5.6,33.7
Formula:

where
 are data points,
are data points,
 is the mean and n is the number of observations.
is the mean and n is the number of observations.
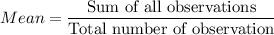
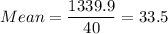
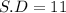 (given)
(given)
n = 40
Confidence interval:
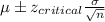
Putting the values, we get,