Question

A car with mass m=1.43e3 kg is initially traveling directly east with a speed ????????=25.0 m/s. It crashes into the rear end of a truck with mass ????=9000 kg moving in the same direction with speed ????????=20.0 m/s. Immediately after the collision the car has a speed ????????=18.0 m/s in its original direction (the two do not stick together in this case). (a) What is the speed of the truck immediately after the collision?

Answer 1

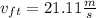`v_(ft) = 21.11 (m)/(s)` : Speed of the truck immediately after the collision , to the east.

Step-by-step explanation:

Theory of collisions

Linear momentum is a vector magnitude (same direction and direction as velocity) and its magnitude is calculated like this:

P=m*v

where

P:Linear momentum

m: mass

v:velocity

There are 3 cases of collisions : elastic, inelastic and plastic.

For the three cases the total linear momentum quantity is conserved:

P₀=Pf Formula (1)

P₀ :Initial linear momentum quantity

Pf : nitial linear momentum quantity

Nomenclature and data

mc: car mass= 1.43*10³ kg = 1430kg

V₀c: initial car speed, = 25.0 m/s

Vfc: final car speed = 18.0 m/s

mt: truck mass = 9000 kg

V₀t: initial truck speed, = 20.0 m/s

Vft: final truck speed

Problem development

For this problem the collision is inelastic because after the collision the objects are deformed .

Because the known speeds go east they are positive, we assume that the truck continues moving east after the collision and its speed will also be positive:

We apply formula (1)

P₀=Pf

mc*V₀c+mt*V₀t=mc*Vfc+mt*Vft

1430*25+9000*20=1430*18+9000*Vft

215750=25740+9000*Vft

`v_(ft) =(215750-25740)/(9000) = 21.11 (m)/(s)`

`v_(ft) = 21.11 (m)/(s)`

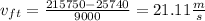
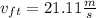
Because the response was positive the truck moves east after the collision