Answer: 0.50477
Explanation:
Given : The sugar content of the syrup is canned peaches is normally distributed.
We assume the can is designed to have standard deviation
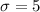 milligrams.
milligrams.
The sampling distribution of the sample variance is chi-square distribution.
Also,The data yields a sample standard deviation of
 milligrams.
milligrams.
Sample size : n= 10
Test statistic for chi-square :
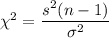
i.e.
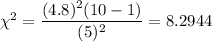
Now, P-value =
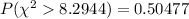 [By using the chi-square distribution table for p-values.]
[By using the chi-square distribution table for p-values.]
Hence, the chance of observing the sample standard deviation greater than 4.8 milligrams = 0.50477