Question

The fraction of defective integrated circuits produced in a photolithography process is being studied. A random sample of 300 circuits is tested, revealing 17 defectives. (a) Calculate a 95% two-sided confidence interval on the fraction of defective circuits produced by this particular tool. Round the answers to 4 decimal places. less-than-or-equal-to p less-than-or-equal-to (b) Calculate a 95% upper confidence bound on the fraction of defective circuits. Round the answer to 4 decimal places. p less-than-or-equal-to

Answer 1

(a) The confidence interval is: 0.0304 ≤ π ≤ 0.0830.

(b) Upper confidence bound = 0.0787

Explanation:

(a) The confidence interval for p (proportion) can be calculated as

`p \pm z*\sigma_(p)`

`\sigma=\sqrt{(\pi*(1-\pi))/(N) }\approx\sqrt{(p(1-p))/(N) }`

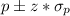
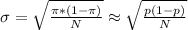
NOTE: π is the proportion ot the population, but it is unknown. It can be estimated as p.

`p=17/300=0.0567\\\\\sigma=\sqrt{(p(1-p))/(N) }=\sqrt{(0.0567(1-0.0567))/(300) }=0.0134`

For a 95% two-sided confidence interval, z=±1.96, so

`\\LL = p-z*\sigma=0.0567 - (1.96)(0.0134) = 0.0304\\UL =p+z*\sigma= 0.0567 + (1.96)(0.0134) = 0.0830\\\\`

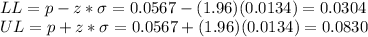
The confidence interval is: 0.0304 ≤ π ≤ 0.0830.

(b) The confidence interval now has only an upper limit, so z is now 1.64.

`UL =p+z*\sigma= 0.0567 + (1.64)(0.0134) = 0.0787`

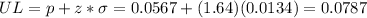
The confidence interval is: -∞ ≤ π ≤ 0.0787.