Question

The question: Bob and Larry combine to run a 7,460-meter race in 27 minutes. Bob runs an average speed of 300 meters per minute, and Larry runs an average speed of 260 meters per minute. How many minutes does each of them run?

The wording of this question confuses me.

I don't understand how it should be set up (this is systems of equations).

Answer 1

Bob runs for 11 minutes and Larry runs for 16 minutes

Explanation:

- Bob and Larry combine to run a 7,460-meter race in 27 minutes

- The total distance = 7460 m

- The total time = 27 minutes

- Bob runs an average speed of 300 meters per minute

- Larry runs an average speed of 260 meters per minute

- Assume that Bob runs d meter, then Larry runs distance = 7460 - d

- The time = distance ÷ speed

∵ Bob runs d meter by 300 meters/min.

∴ Bob time's =
`(d)/(300)`

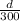
∵ Larry runs 7460 meter by 260 meters/min.

∴ Larry time's =
`(7460-d)/(260)`

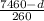
∵ The total time = 27 minutes

∴
`(d)/(300)+(7460-d)/(260)=27`

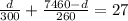
- Multiply all terms by 7800 to cancel the denominator

∴ 26d + 30(7460 - d) = 210600

∴ 26d + 223800 - 30d = 210600

- Add like terms in left hand side

∴ -4d + 223800 = 210600

- Subtract both sides by 223800

∴ -4d = -13200

- Divide both sides by -4

∴ d = 3300

∵ d represents the Bob distance

∴ Bob runs 3300 meters

∵ 7460 - d represents Larry distance

∴ Larry runs = 7460 - 3300 = 4160 meters

∵ Bob time's =
`(d)/(300)`

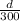
∴ Bob time's =
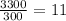`(3300)/(300)=11` minutes

∵ Larry time's =
`(7460-d)/(260)`

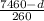
∴ Larry time's =
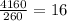`(4160)/(260)=16` minutes

* Bob runs for 11 minutes and Larry runs for 16 minutes