Answer:
(A)
 with
with
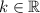 .
.
(B)
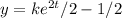 with
with
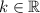
(C)
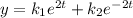 with
with

(D)
 with
with
 ,
,
Explanation
(A) We can see this as separation of variables or just a linear ODE of first grade, then
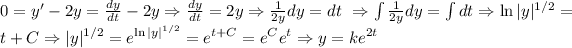 . With this answer we see that the set of solutions of the ODE form a vector space over, where vectors are of the form
. With this answer we see that the set of solutions of the ODE form a vector space over, where vectors are of the form
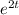 with
with
 real.
real.
(B) Proceeding and the previous item, we obtain
 . Which is not a vector space with the usual operations (this is because
. Which is not a vector space with the usual operations (this is because
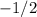 ), in other words, if you sum two solutions you don't obtain a solution.
), in other words, if you sum two solutions you don't obtain a solution.
(C) This is a linear ODE of second grade, then if we set
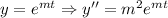 and we obtain the characteristic equation
and we obtain the characteristic equation
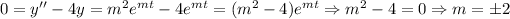 and then the general solution is
and then the general solution is
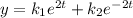 with
with
 , and as in the first items the set of solutions form a vector space.
, and as in the first items the set of solutions form a vector space.
(D) Using C, let be
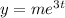 we obtain that it must satisfies
we obtain that it must satisfies
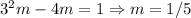 and then the general solution is
and then the general solution is
 with
with
 , and as in (B) the set of solutions does not form a vector space (same reason! as in (B)).
, and as in (B) the set of solutions does not form a vector space (same reason! as in (B)).