Answer:
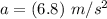
Step-by-step explanation:
Given that,
An object starts from rest at the origin (x₀ = 0) and travels in a straight line with a constant acceleration (a = constant).
The relation between the position (x) and time (t) is given by :
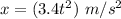
Let v is the velocity of the object.
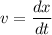

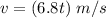
Let a is the acceleration of the object. It is given by :
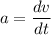
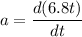
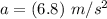
So, the acceleration of the object is
 . Hence, this is the required solution.
. Hence, this is the required solution.