Question

A wire of length L and cross-sectional area A has resistance R.What will be the resistance Rstretched of the wire if it is stretched to twice its original length? Assume that the density and resistivity of the material do not change when the wire is stretched.

Answer 1

Step-by-step explanation:

The resistance of a wire having length L and cross-sectional area A is given by :

`R=(\rho L)/(A)`

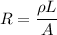
Where

`\rho` is the resistivity of the material.

Let R' is the resistance of the wire when it is stretched to twice its original length, L' = 2L

Since, the volume remains constant. So,

`AL=A'L'`

`A'=(A)/(2)`

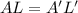
The new resistance is given by :

`R'=(\rho (2L))/(A/2)`..............(2)

`(R)/(R')=(1)/(4)`

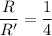
R' = 4R

So, the resistance of the wire becomes four time of the original resistance. Hence, this is the required solution.